- Inovações
- Artigos sobre o uso de PCI
- Comercio pela Carteira
Optimização da carteira pelo método PQM (parte1)
Pesquisa da estrutura optimal dos ativos na carteira, por suposto é um problema dificil. Pela uma parte muito depende dos parametros dos ativos que encontram-se incluidos na carteira, pela outra parte das preferências e restrições do investidor.No entanto a teria moderna financeira e os novos métodos de análise e vendas facilitam muito este processo.
Um dos exemplos da realização da carteira atual pode ser observado o Método de Cotação do Carteiras, que permite construir e analisar uma variedade imensa das carteiras, construidas de uma variedade dos ativos. Devemos dizer que o valor das possibilidades de analise ve-se não somente em observação Além disso, o valor de oportunidades para a análise não é somente para observar a variação do valor absoluto da carteira, mas também para estudar o comportamento da carteira em relação ao mercado ou, por exemplo, uma carteira alternativa que permite realizar rapidamente as decisões de investimento. O resultado da aplicação do método é a criação de novas unidades financeiras – instrumentos sintéticos (com o nome técnico PCI - instrumento composto pessoal).
Neste artigo limitamo-nos com conjunto 6 ativos da empresa americana , os quais, da primeira vista, mostraram resultados relativamente satisfatorios durante os ultimos anos. Com a ajuda de metodo GeWorko compomos a carteira, que mostrou um crescimento significativo em periodo de post-crise. Na Nossa escolha entraram(De forma voluntaria:
- Walt Disney Company (20%)
- Home Depot Inc. (20%)
- Honeywell International Inc. (15%)
- International Business Machines Corporation (15%)
- Coca-Cola Company (10%)
- McDonald’s Corporation (20%)
Com a comparação da dinamica de carteira com o mercado(como o mercado apresenta-se relativamente o índice Dow Jones Industrial Average, que inclui todas as ações)resultou que a carteira sistematicamente batia o índice antes e depois da crise, enquanto ele encontrava-se no período de recuperação. Resultando em uma questão de segundos PCI gráfico ilustra muito bem o comportamento da carteira em relação ao índice de:
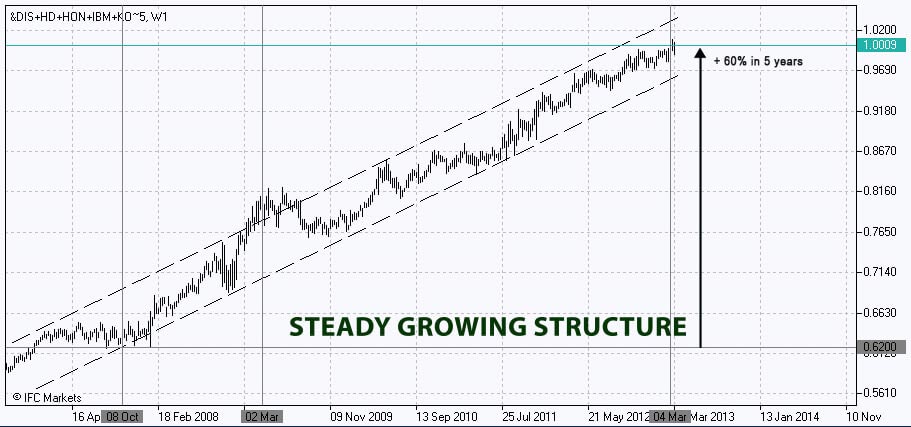
Apesar da seleção alentadora dos ativos que incorporam-se nos ativos, ainda não sabemos se a carteira de ativos, vai ter sucesso absoluto isto é, se há outros pesos, proporcionando um grau de risco mais baixo no mesmo nível de rentabilidade, ou uma maior taxa de retorno ao mesmo nível de risco. Se pudermos encontrar uma tal carteira, certamente será melhor para o investidor racional, do que uma carteira com pesos aleatórios.
No entanto, a determinação da carteira ótima para o investidor, como mencionado acima, vai depender das preferências individuais e restrições. Sem a presença dos requisitos específicos de desempenho para a carteira, não podemos saber se, por exemplo, para um investidor com uma carteira de países de alta renda, mas também maiores níveis de risco, preferiu o portfolio de origem. Neste contexto, para fins de análise, a carteira ideal é chamado de uma carteira que teria o máximo de retorno por unidade de risco. Isto é conhecido como o índice de Sharpe.
Ao contrário de sua versão tradicional, o qual mostra a relação entre o prêmio de risco do índice de risco, nos restringimos à relação entre os retornos da carteira de risco, sem ajuste para a taxa livre de risco. Esta simplificação não afeta as conclusões que irá comparar a eficácia das carteiras de investimento alternativos.
Para iniciar voltamos à carteira original com dados aleatoriamente de pesos e definimos seus parâmetros de risco e retorno. das carteiras será baseada em dados mensais sobre os preços de fechamento de seis partes para a amostra de Janeiro de 2005 - abril de 2013. Uma vez que o propósito original era comparar a dinâmica do portfólio com o índice (o mercado), decidiu-se aplicar um pouco de uma abordagem não convencional e ajustar o preço mensal de fechamento das ações dividindo-se os valores correspondentes do índice. Com base nos incrementos dos logaritmos rendimento foi calculado o retorno mensal média e desvio padrão de retorno para os seis conjuntos de dados. Os resultados dos cálculos são mostrados no quadro a seguir:
| DIS | HD | HON | IBM | KO | MCD | |
| Mean Return | 0.49% | 0.24% | 0.40% | 0.42% | 0.35% | 0.77% |
| StDev | 4.25% | 5.73% | 4.51% | 4.53% | 3.95% | 4.09% |
| Sharpe Ratio | 0.11 | 0.04 | 0.09 | 0.09 | 0.09 | 0.19 |
Resultou que a maior parte (0,77%), do rendimento médio mensal (em comparação com o índice) mostraram populações de MDC, a menor - Acções HD (0,24%). O menor desvio de padrão das ações f marcaram-se KO (3,95%), a maior - estoques HD (5,73%). Além disso, calculou-se uma versão simplificada do Sharpe, que mostra a proporção de retorno para activos de risco. O maior índice (0,19) em ações MCD, que apresentou o melhor valor de retorno por unidade de risco. Este facto permite-nos supor que ele estará em estoque MCD o maior peso na carteira "ótima". Para continuar a análise também terá as seis características da relação entre um ativo - fatores de covariância. A matriz de covariância é calculada com a mesma amostra de dados mensais.
Tendo todos os parâmetros necessarios de entrada e assumindo que os valores obtidos tanto de retorno como de desvio de padrão para os seis papéis são as melhores estimativas de retornos e riscos esperados, podemos começar a construir carteiras. Lembre-se que os dados originais foram ajustados para o valor do índice, de modo que as carteiras que nós temos já vai refletir o comportamento em relação ao mercado.
primeira carteira (P1), o que teremos será o ponto de partida para uma combinação mais bem-sucedidos de ativos. Esta carteira com pesos aleatórios, o gráfico era desde o início. Conhecer os parâmetros de risco e retorno de seis títulos incluídos em sua composição, o seu peso e da matriz de covariância, podemos calcular o retorno médio mensal da carteira e seu desvio padrão. É fácil de ver que, ao combinar os bens que conseguiu uma redução significativa no risco. O desvio padrão da carteira P1 é apenas de 1,74%, eo rendimento - 0,46%:
| DIS | HD | HON | IBM | KO | MCD | P1 | |
| Mean Return | 0.49% | 0.24% | 0.40% | 0.42% | 0.35% | 0.77% | 0.46% |
| StDev | 4.25% | 5.73% | 4.51% | 4.53% | 3.95% | 4.09% | 1.74% |
| Sharpe Ratio | 0.11 | 0.04 | 0.09 | 0.09 | 0.09 | 0.19 | 0.26 |
Além disso, quando comparado com qualquer um dos seis carteira de títulos tem um muito maior impacto de retorno por unidade de risco, tal como evidenciado pela Sharpe (0,26), que no final vai determinar a eficácia da carteira.
Agora sabendo características da carteira aleatória , podemos começar a olhar para uma combinação de ativos que melhor atendam às nossas preferências e restrições. Como já mencionado, o principal indicador da carteira ótima, nós escolhemos o índice de Sharpe. Ao alterar o peso dos seis títulos que compõem a carteira, é preciso encontrar uma combinação que corresponderia ao mais alto possível relação risco-recompensa. As únicas limitações sobre a procura de soluções, peça, são o facto de que os pesos não deve ser inferior a zero, e a soma deve ser igual a 100%, a fim de manter a capacidade de comparação carteiras.
A decisão nos leva à seguinte composição da carteira: Como esperávamos, o maior peso (32,67%) receberam ações da MCD, uma vez que teve o índice de Sharpe mais elevado. Então descendente pesos variaram DIS (19,33%), HON (19,04%), HD (10,96%), KO (10,28%) e IBM (7,71%):
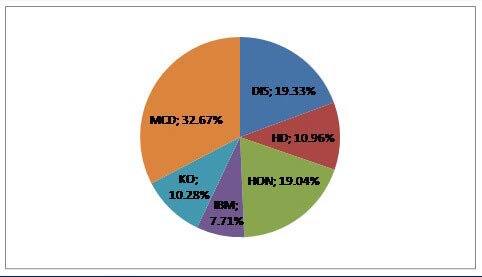
O resultado obtido alterando os pesos para maximizar o índice de Sharpe, a carteira (P2) mostrou claramente um melhor desempenho do que uma carteira com pesos aleatórios (Р1):
| DIS | HD | HON | IBM | KO | MCD | P1 | P2 | |
| Mean Return | 0.49% | 0.24% | 0.40% | 0.42% | 0.35% | 0.77% | 0.46% | 0.52% |
| StDev | 4.25% | 5.73% | 4.51% | 4.53% | 3.95% | 4.09% | 1.74% | 1.72% |
| Sharpe Ratio | 0.11 | 0.04 | 0.09 | 0.09 | 0.09 | 0.19 | 0.26 | 0.30 |
Maximizado o índice de Sharpe para a carteira foi de 0,3 P2. Este valor é superior ao da carteira P1 (0,26), para não mencionar os parâmetros individuais dos activos. Para além disso, estritamente como um indicador foi melhor rendimento (0,52%) e o desvio-padrão (1,72%). Conclusão - obtido através da maximização da carteira Índice de Sharpe é sempre preferível para um investidor racional (lembre-se do pressuposto de nossa análise que os indicadores calculados de risco e retorno são as suas melhores estimativas).
Com a ajuda de ferramentas de PCI, podemos facilmente construir nos encontrou a carteira de "ótimo", introduzindo os pesos obtidos para as seis ações, e correlacionando a parte básica do PCI em comparação com o mesmo valor de uma carteira composta apenas do índice Dow Jones Industrial Average (ver gráfico).
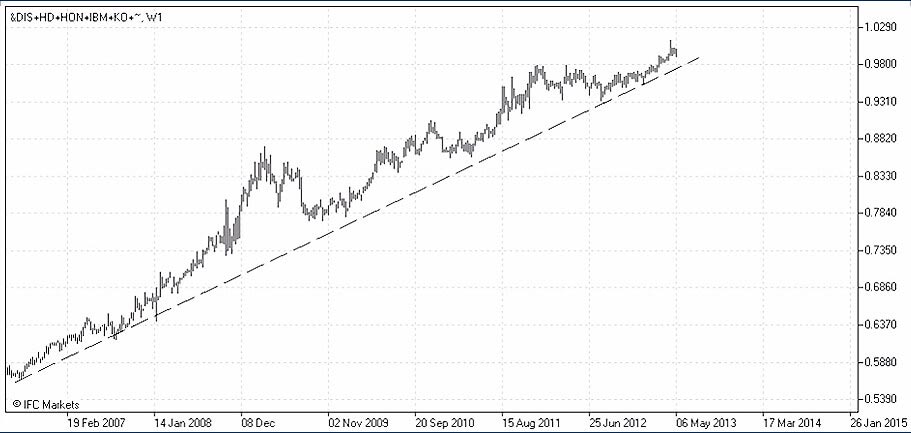
Como no caso anterior com o "random" portfolio P1, ficamos crescendo quase continuamente durante os últimos 7 anos, a estrutura, a volatilidade que está significativamente aumentada em tempos de instabilidade econômica.
No entanto, ressaltamos que esta é a carteira ótima para nós, porque nós escolhemos o índice de Sharpe como uma medida chave da otimização. Nós só podemos dizer que, com os parâmetros de entrada existentes há outra carteira que nos permitiria alcançar rendimentos mais elevados (> 0,52%), para um dado nível de risco (1,72%) e sem carteira, o que seria menos arriscado (<1,72%) para um determinado rendimento (0,52%). No entanto, é possível que um investidor está disposto e tem as possibilidades objetivas para ir para o aumento do risco, a fim de alcançar uma maior taxa de retorno, ou vice-versa, o investidor está buscando portfolio minimamente risco dos ativos disponíveis.
Para a continuação do artigo, consulte a seção "Otimização da Estrutura de Carteira usando o Método PQM (parte 2)"
Artigos Anteriores
- Quarto princípio básico da Teoria de Dow: serviço ao investidor
- Spread de carteira através de futuros contínuos
- Carteira Sharpe– “Três Lideres” - DJIA, S&P500, Nasdaq 100
- Método de Cotação de Carteiras para Análise de Carteiras "Boas" e "Más"
- Otimização de portfólio com a ajuda de metodo PQM (parte 2)
- Construir e Analisar Carteiras | Método de Cotação de Carteiras (PQM)
